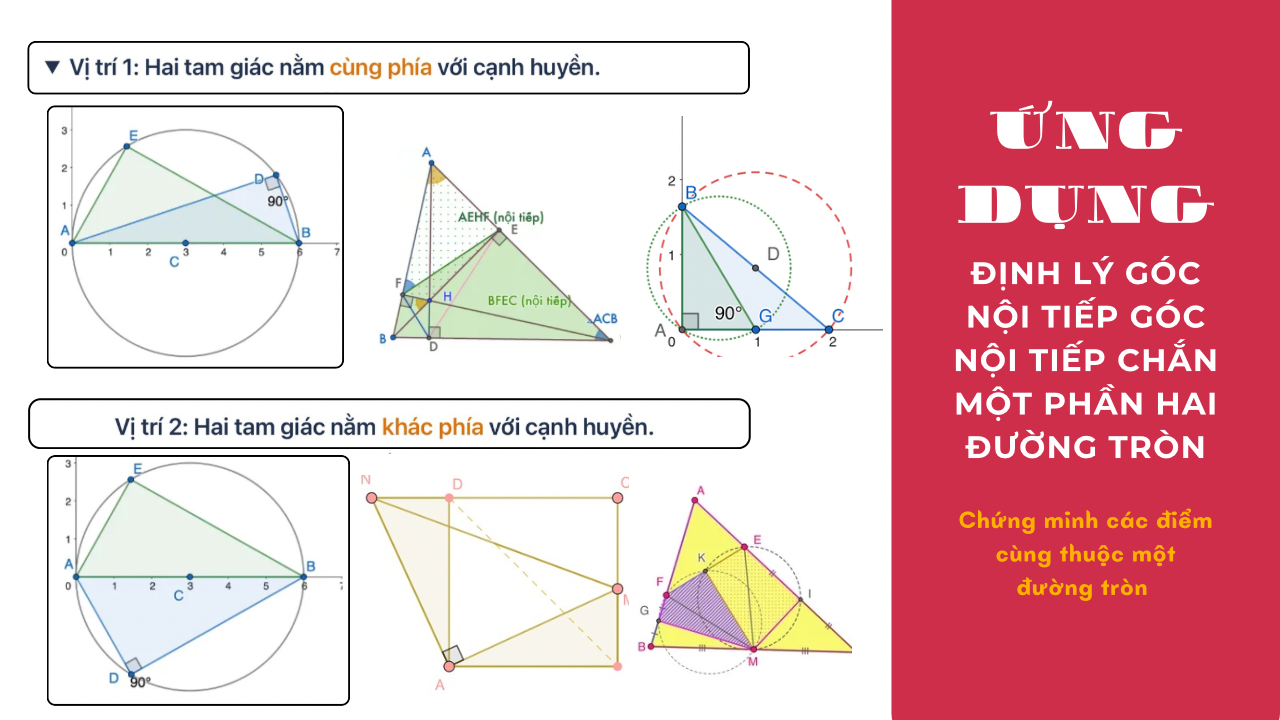
Ứng Dụng Định Lý Góc Nội Tiếp Chắn Nửa Đường Tròn: Chứng Minh Các Điểm Cùng Thuộc Một Đường Tròn
Bài viết cung cấp kiến thức cơ bản và các ứng dụng thực tế của định lý góc nội tiếp chắn nửa đường tròn. Từ phát biểu định lý, chứng minh lý thuyết đến các ví dụ minh họa cụ thể, bạn sẽ hiểu cách chứng minh các điểm cùng thuộc một đường tròn một cách rõ ràng và dễ dàng.