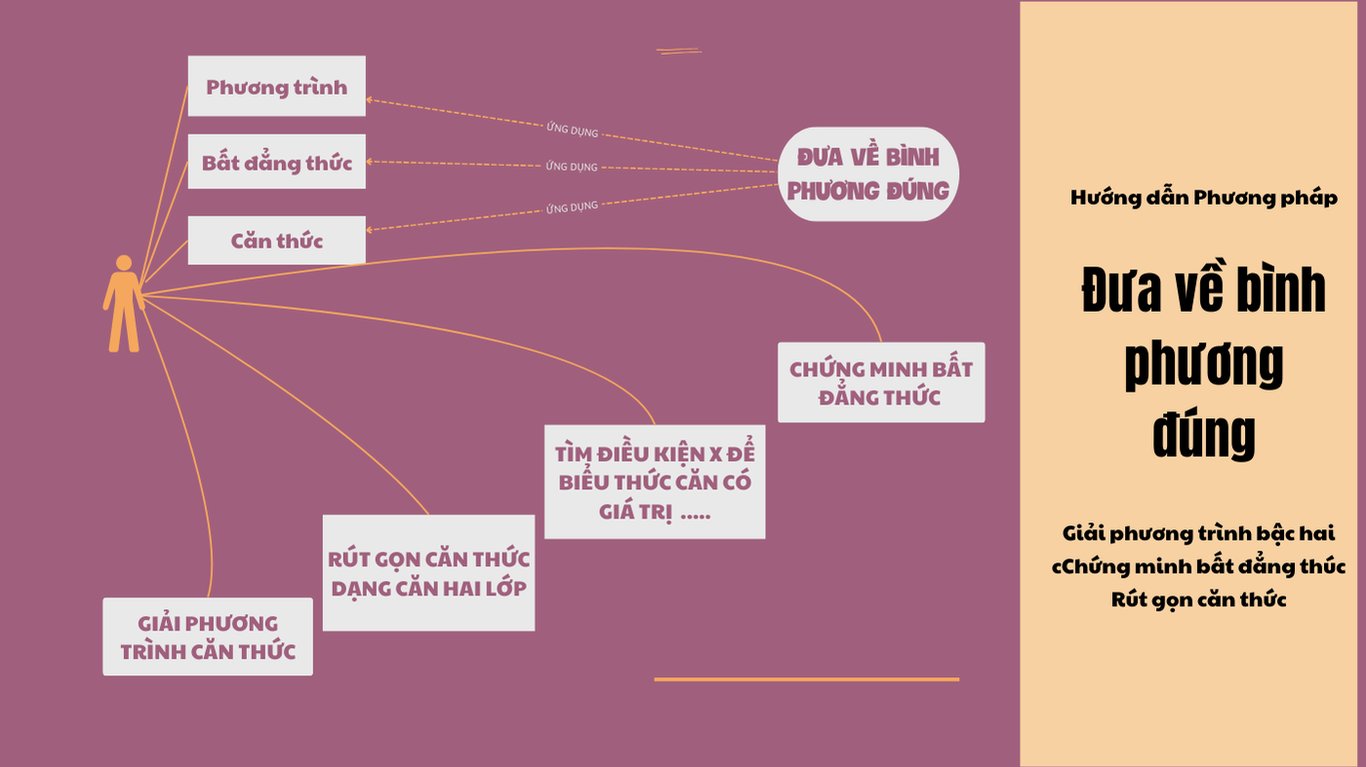
Kỹ thuật đưa về bình phương đúng trong giải phương trình, căn thức và bất đẳng thức | Toán Cô Diễm
Phương pháp đưa về bình phương đúng là một kỹ thuật chuyển đổi một biểu thức bậc hai thành bình phương của một biểu thức. Cách này giúp bạn dễ dàng tìm được nghiệm mà không cần dùng công thức nghiệm tổng quát, ngoài ra còn đặc biệt hữu dụng ch Bài viết sẽ hướng dẫn chi tiết các bước thực hiện cùng ví dụ minh họa cụ thể.