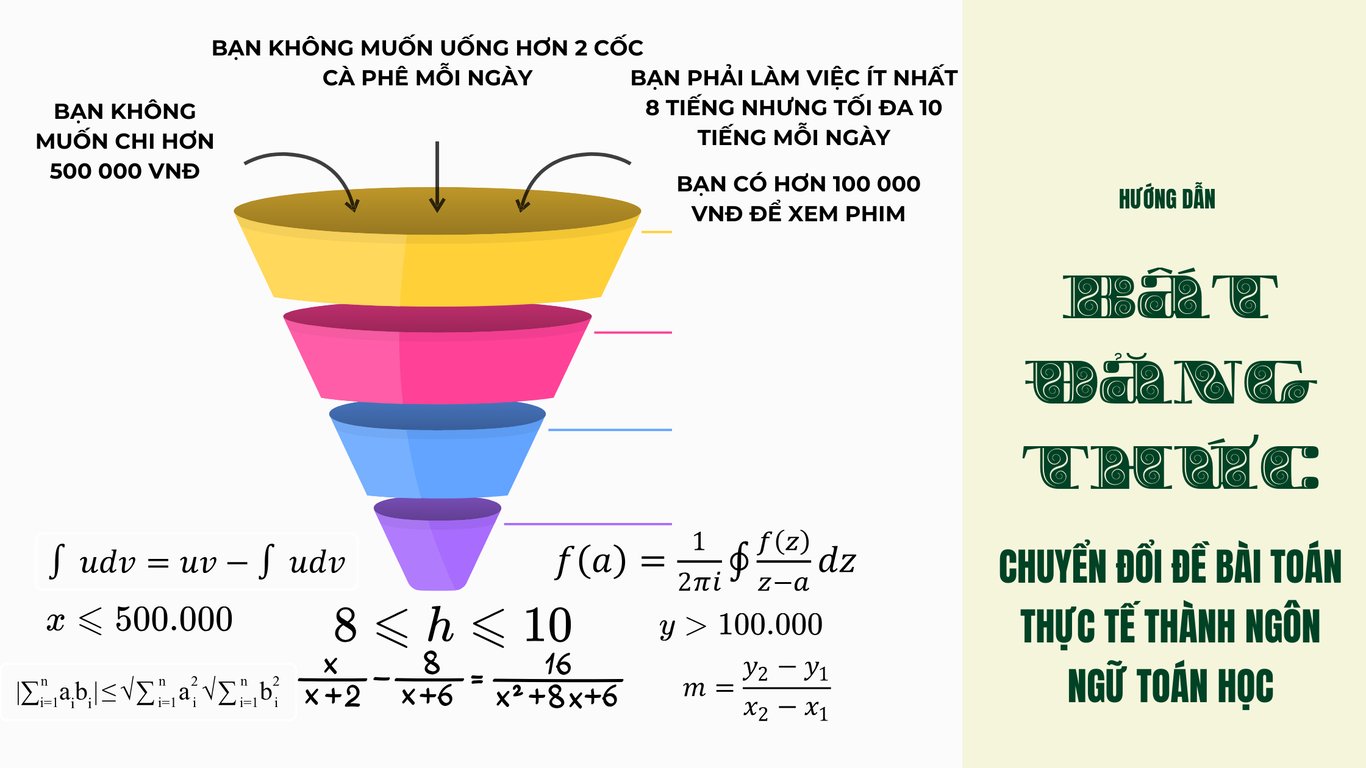
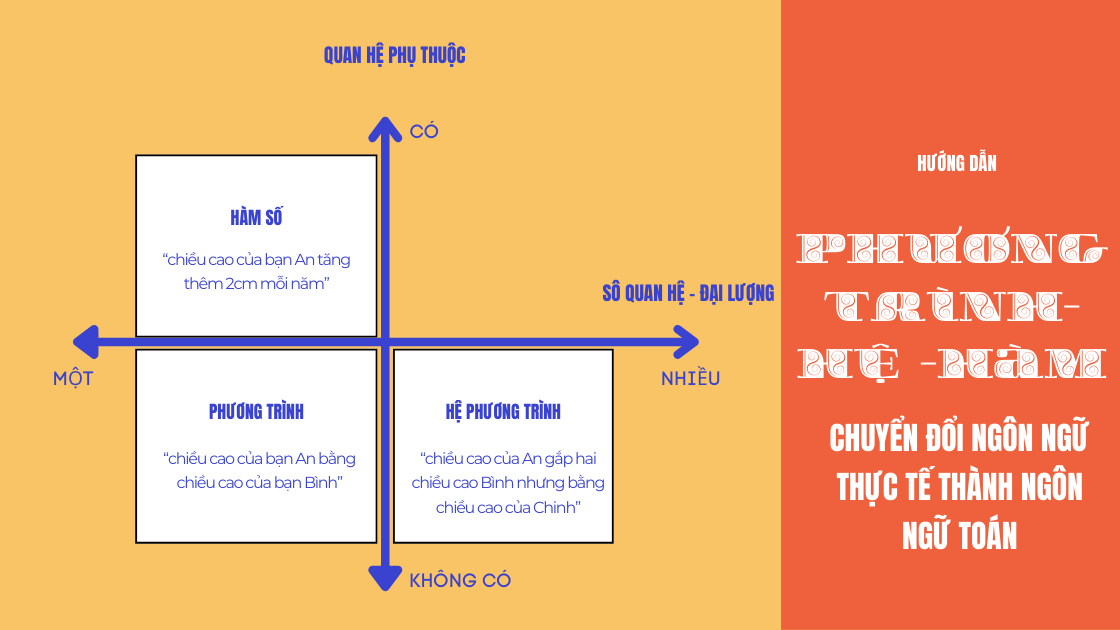
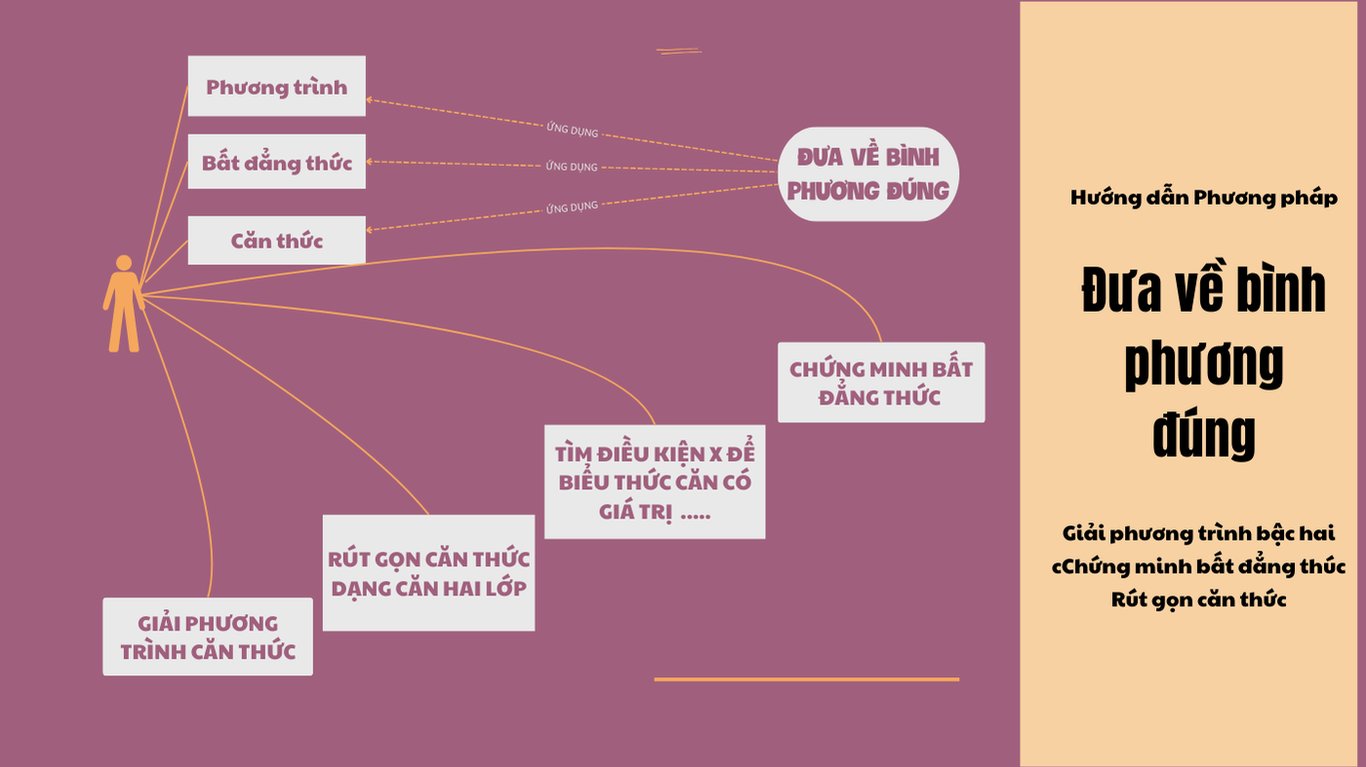
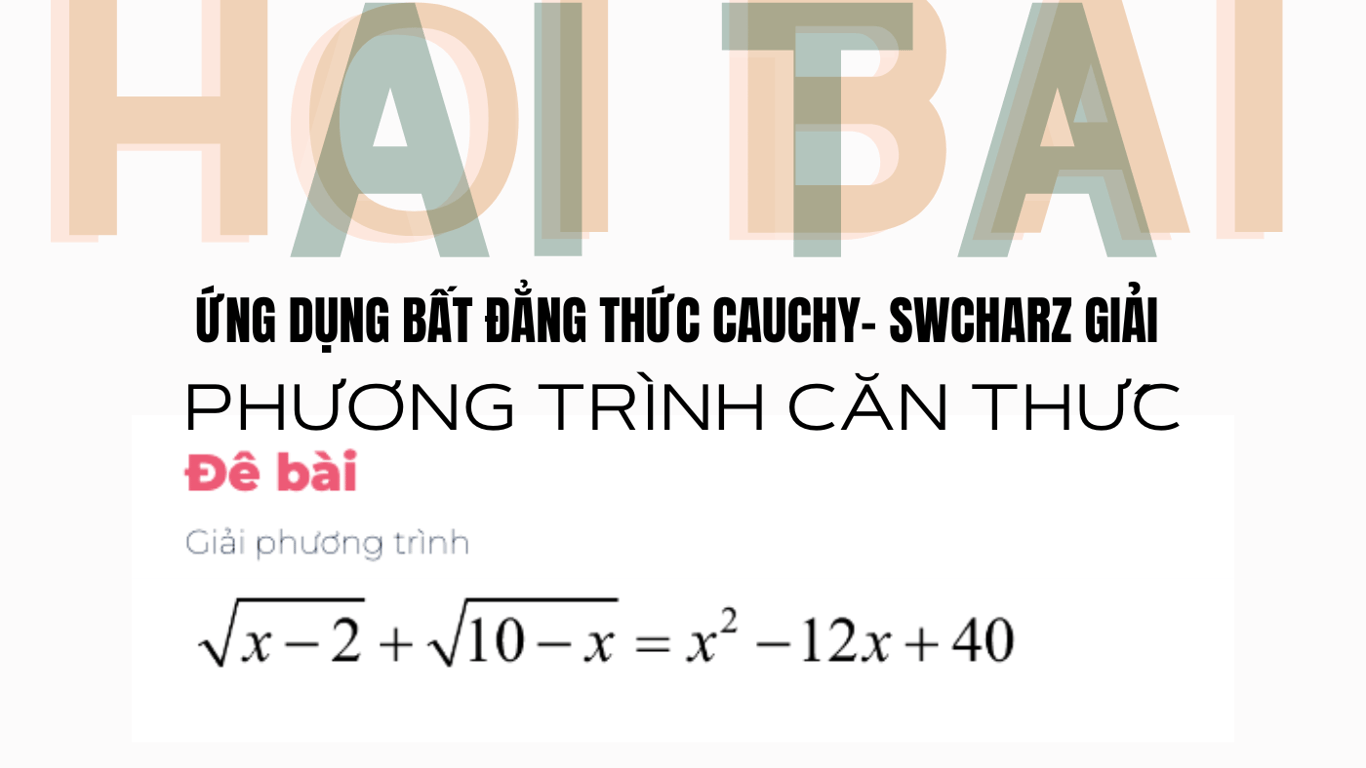Hướng Dẫn Giải Phương Trình Chứa Căn với Tham Số Nguyên | Toán Cô Diễm
Toán Cô Diễm hướng dẫn chi tiết cách giải phương trình chứa căn với tham số mmm nguyên. Bài viết bao gồm các bước rút gọn, tính delta, và kiểm tra điều kiện nghiệm nguyên, giúp học sinh nắm vững kỹ thuật giải toán nâng cao.