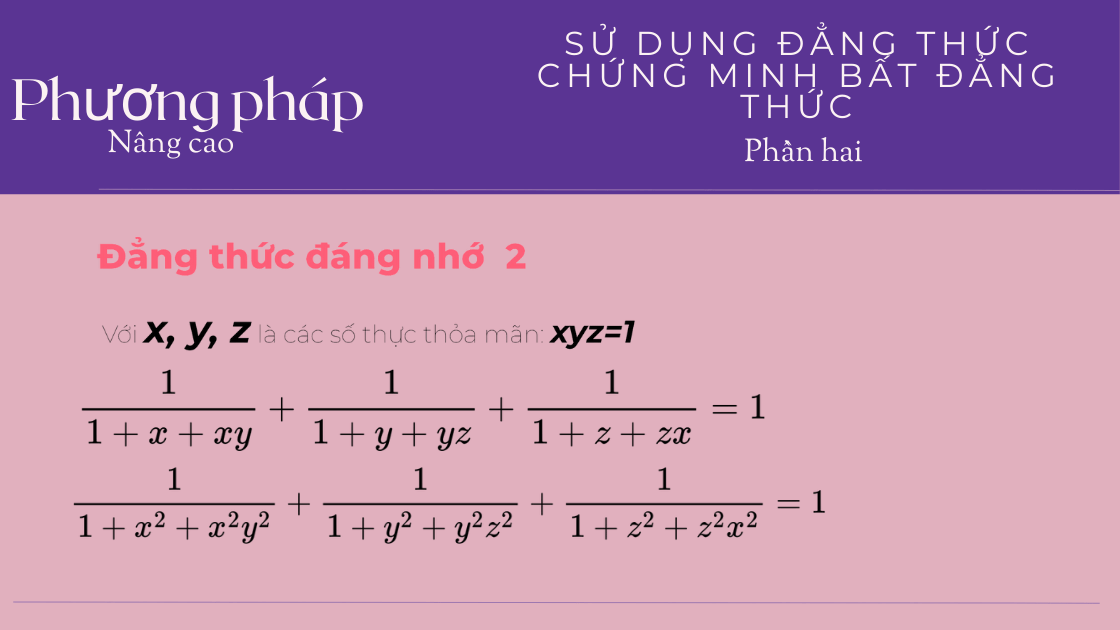
Sử Dụng Đẳng Thức Để Chứng Minh Bất Đẳng Thức (Phần 3)
Bài viết trình bày phương pháp sử dụng các đẳng thức quen thuộc trong chứng minh bất đẳng thức, kèm theo ví dụ minh họa chi tiết và bài tập vận dụng. Đây là phần 1 trong chuỗi chuyên đề dành cho học sinh yêu thích toán học, đặc biệt là các bạn đang ôn thi vào lớp chuyên